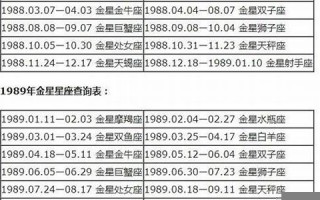
九宫图算法是一种常见的数学算法,广泛应用于数字图像处理、数据分析、人工智能等领域。它通过将问题划分为九个部分,使得复杂的数学问题能够在一定规则下得到简化。这种算法不仅能提高计算效率,还能在处理大型数据时保证结果的准确性。本文将全面介绍九宫图算法的基本原理、应用场景及其优势,帮助读者更好地理解和运用这一算法。
九宫图算法的基本原理
九宫图算法是通过将问题划分为九个区域,利用这些区域的交集与排除关系,简化问题的复杂度。在传统的数字图像处理中,九宫图算法常常用于对图像进行分块处理。每个小块的数值代表了图像的一部分,通过优化这些小块的计算,可以提高整体图像处理的效率。该算法在数据压缩、特征提取等领域也有着重要的应用。
九宫图算法的实现方法
在实现九宫图算法时,首先需要将数据集划分成九个部分。这些部分可以是均匀分布的,也可以根据具体需求进行调整。每个部分的内容会进行独立的处理,然后根据算法规则进行组合。通过这种方式,九宫图算法能够在每个小块上并行处理数据,从而提高整体的计算速度和准确性。

九宫图算法的应用场景
九宫图算法广泛应用于多个领域,尤其是在图像处理、人工智能、数据分析等方面。在图像处理中,九宫图算法被用来分块处理图像,提高图像分析和识别的速度与准确性。在数据分析中,九宫图算法帮助分析师高效地提取数据特征,简化复杂数据的处理过程。此外,人工智能领域也常通过九宫图算法进行问题优化,提升计算模型的性能。
九宫图算法的优势与挑战
九宫图算法的主要优势在于其计算效率和处理精度。通过划分小块进行并行计算,能够有效减少计算量和时间。同时,该算法能够适应大规模数据处理,具有较强的扩展性。然而,九宫图算法在某些情况下也面临着计算复杂度过高和数据划分不均等挑战。因此,在实际应用中需要根据具体情况进行优化。
总结起来,九宫图算法作为一种高效的数学算法,在多个领域得到了广泛应用。它通过将问题划分为九个小块,从而实现高效的数据处理。尽管存在一定的挑战,但凭借其出色的计算能力和适用性,九宫图算法仍然是现代数据处理领域中的重要工具。掌握这一算法的原理与应用,将为相关领域的研究和发展提供有力支持。